Tahukah kamu apa yang dimaksud dengan hipotesis dan bagaimana cara membuat hipotesis dengan baik dan benar? Dalam statistik, hipotesis dapat diartikan sebagai pernyataan statistik tentang parameter populasi. Sangat penting memahami pengertian lengkapnya, olehnya yuk simak pengertian hipotesis secara mendalam, sekarang!
Pengertian Hipotesis
Hipotesis berasal dari kata hupo dan thesis. Hupo artinya sementara/lemah kebenarannya dan thesis artinya pernyataan/teori. Dengan demikian hipotesis berarti pernyataan sementara yang perlu diuji kebenarannya.
Untuk menguji kebenaran sebuah hipotesis digunakan pengujian yang disebut uji hipotesis. Dalam kehidupan kita sehari-hari, tanpa kita sadari bahwa hipotesis ini sering kita lakukan.
Pengujian hipotesis dapat berguna untuk membantu tentang pengambilan keputusan terhadap hipotesis yang diajukan, seperti adanya perbedaan atau hubungan dua variabel tersebut cukup meyakinkan untuk ditolak atau tidak ditolak.
Prinsip uji hipotesis adalah melakukan perbandingan antara nilai sampel (data hasil penelitian) dengan nilai hipotesis (nilai populasi) yang diajukan.
Peluang untuk diterima dan ditolaknya suatu hipotesis tergantung besar ke-cilnya perbedaan antara nilai sampel dengan nilai hipotesis. Bila perbedaan tersebut cukup besar, maka peluang untuk menolak hipotesis juga besar.
Sebaliknya bila perbedaan tersebut kecil, maka peluang untuk menolak hipotesis menjadi kecil. Jadi semakin besar perbedaan antara nilai sampel dengan nilai hipotesis, semakin besar untuk menolak hipotesis. Dan kesimpulan yang didapat dari hasil pengujian hipotesis ada dua kemungkinan, menolak hipotesis dan menerima hipotesis (gagal menolak hipotesis).
Misalnya, ketika kita akan berangkat kerja dengan cuaca hujan, dimana daerah yang kita lewati adalah rawan banjir. Maka kita akan menduga-duga apakah saat ini tergenang banjir atau tidak yang dapat menghambat perjalanan menuju tempat kerja. Sehingga bila kita ingin mengetahui banjir atau tidak, maka harus di buktikan dengan mendatangi jalan menuju tempat kerja tadi.
Demikian juga di kebidanan, mungkin sobat pernah menduga-duga tentang mengapa sebagian besar ibu hamil menderita anemia.
Dan pemikiran sobat akan berkembang ke arah yang perlu digali, misalnya apakah karena pola makan yang tidak baik atau ibu hamil ini tidak mau meminum zat besi yang diberikan oleh petugas.
Pemikiran-pemikiran tersebut adalah merupakan hipotesis, dan untuk megetahui jawabannya harus dibuktikan melalui uji hipotesis.
Keyakinan ini didasarkan pada besarnya peluang untuk memperoleh hubungan tersebut secara kebetulan (by chance). Semakin kecil peluang adanya kebetulan, semakin besar keyakinan bahwa hubungan tersebut memang ada.
Jenis Hipotesis
Jenis hipotesis dapat dilihat pada bagan berikut:
1. Hipotesis Nol (Ho)
Hipotesis Nol (Ho) adalah hipotesis yang menyatakan tidak ada perbedaan kejadian antara kedua kelompok. Atau hipotesis yang menyatakan tidak ada hubungan antara variabel satu dengan variabel lain.
Berikut contoh hipotesis nol:
- Tidak ada perbedaan berat badan bayi antara bayi yang dilahirkan dari ibu yang anemia dengan bayi yang dilahirkan dari ibu yang tidak anemia.
- Tidak ada hubungan berat badan bayi dengan anemia.
2. Hipotesis Alternatif (Ha)
Hipotesis Alternatif (Ha) merupakan pernyataan terbalik dari hipotesis nol, yaitu hipotesis yang menyatakan ada perbedaan kejadian antara kedua kelompok. Atau hipotesis yang menyatakan ada hubungan antara variabel satu dengan variabel lain.
Berikut contoh hipotesis alternatif:
- Ada perbedaan berat badan bayi antara bayi yang dilahirkan dari ibu yang anemia dengan bayi yang dilahirkan dari ibu yang tidak anemia.
- Ada hubungan berat badan bayi dengan anemia.
Bentuk hipotesis alternatif akan menentukan arah uji statistik apakah satu arah (one tail) atau dua arah (two tail).
Hipotesis alternatif satu sisi adalah bila hipotesis alternatifnya menyatakan adanya perbedaan dan ada pernyataan yang mengatakan hal yang satu lebih tinggi/rendah daripada hal yang lain.
Sebagai contoh, berat badan bayi dari ibu hamil anemia lebih kecil dibandingkan berat badan bayi dari ibu hamil yang tidak anemia.
Hipotesis alternatif dua sisi adalah hipotesis alternatif yang hanya menyatakan perbedaan tanpa melihat apakah hal yang satu lebih tinggi/rendah dari hal yang lain.
Sebagai contoh, berat badan bayi dari ibu hamil yang anemia berbeda dibandingkan berat badan bayi dari ibu hamil yang tidak anemia.
Kesalahan Pengambilan Keputusan dan Tingkat Kemaknaan
Dalam pengujian hipotesis kita selalu dihadapkan suatu kesalahan pengambilan keputusan. Hal ini disebabkan karena hampir seluruh penelitian menggunakan sampel dan sangat sulit bahkan tidak mungkin melakukan observasi pada seluruh populasi.
Ada dua jenis kesalahan pengambilan keputusan dalam uji statistik, yaitu kesalahan tipe I (α) dan kesalahan tipe II (β).
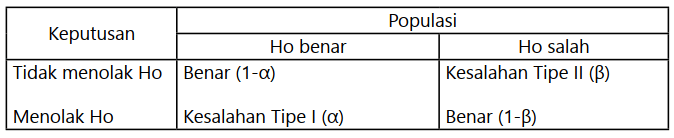
1. Kesalahan tipe I (α)
Kesalahan tipe I (α) merupakan kesalahan menolak Ho, padahal sesungguhnya Ho benar. Artinya menyimpulkan adanya perbedaan, padahal sesungguhnya tidak ada perbedaan.
Peluang kesalahan tipe I adalah α atau sering disebut tingkat signifikansi/tingkat kemaknaan (significance level). Sebaliknya, peluang untuk tidak membuat kesalahan tipe I adalah 1-α, yang disebut dengan tingkat kepercayaan (confidence level).
Dalam melakukan uji hipotesis nilai α (alpha) inilah yang digunakan untuk menentukan apakah hipotesis nol ditolak atau gagal ditolak.
Jadi, Tingkat kemaknaan atau nilai α dapat diartikan sebagai batas maksimal kita salah menyatakan adanya perbedaan.
Penentuan nilai α tergantung dari tujuan dan kondisi penelitian. Nilai α yang sering digunakan adalah 10%, 5%, atau 1%. Untuk bidang kesehatan masyarakat biasanya 5%, namun bila untuk pengujian obat-obatan atau penelitian klinik batas toleransi kesalahan harus lebih kecil yaitu 1% karena mengandung risiko yang fatal.
2. Kesalahan tipe II (β)
Kesalahan tipe II (β) merupakan kesalahan tidak menolak Ho, padahal sesungguhnya Ho salah. Artinya menyimpulkan tidak ada perbedaan, padahal sesungguhnya ada perbedaan.
Peluang untuk tidak membuat kesalahan tipe II adalah sebesar 1-β, dan dikenal sebagai tingkat kekuatan uji (power of the test).
Kekuatan uji (power of the test) merupakan peluang untuk menolak Ho ketika Ho memang salah. Atau dengan kata lain, kemampuan untuk mendeteksi adanya perbedaan bermakna antara kelompok-kelompok yang diteliti ketika perbedaan-perbedaan itu memang ada.
Prosedur Pengujian Hipotesis
Langkah-langkah dalam pengujian hipotesis dapat adalah berikut ini :
1. Menetapkan hipotesis
Sauadara dapat menetapkan hipotesis nol (Ho) dan hipotesis alternatifnya (Ha) berdasarkan hipotesis penelitian yang sobat buat.
Sebagai contoh, Ho : P1 = P2 (Tidak ada perbedaan berat badan bayi antara bayi yang dilahirkan dari ibu yang anemia dengan bayi yang dilahirkan dari ibu yang tidak anemia) Ha : P1 ≠ P2 (ada perbedaan berat badan bayi antara bayi yang dilahirkan dari ibu yang anemia dengan bayi yang dilahirkan dari ibu yang tidak anemia).
2. Menentukan uji statistik yang sesuai
Ada beragam jenis uji statistik yang dapat digunakan. Setiap uji statistik mempunyai persyaratan tertentu yang harus dipenuhi.
Oleh karena itu, harus digunakan uji statistik yang tepat sesuai dengan data yang diuji. Jenis uji statistik sangat tergantung pada:
- Jenis variabel yang akan dianalisis.
- Jenis data apakah dependen atau independent.
- Jenis distribusi data populasinya
Sebagai gambaran, jenis uji statistik untuk mengetahui perbedaan rata-rata akan berbeda dengan uji statistik yang digunakan untuk mengetahui proporsi/persentase.
Uji beda rata-rata menggunakan uji T atau anova sedangkan uji statistik untuk mengetahui perbedaan proporsi digunakan uji kai kuadrat.
3. Menentukan tingkat kemaknaan
Seperti telah dibahas di atas, bahwa penentuan nilai α (alpha) tergantung pada tujuan penelitian. Untuk bidang kesehatan masyarakat termasuk pelayanan kebidanan biasanya menggunakan nilai α 5%.
4. Penghitungan uji statistik
Penghitungan uji statistik adalah menghitung data sampel ke dalam uji hipotesis yang sesuai. Misalnya, kalau ingin menguji perbedaan proporsi antara dua kelompok, data hasil pengukuran dimasukkan ke rumus uji kai kuadrat.
Dari hasil perhitungan tersebut kemudian dibandingkan dengan nilai populasi untuk mengetahui apakah ditolak atau gagal menolak hipotesis.
5. Keputusan Uji Statistik
Hasil pengujian statistik akan menghasilkan dua kemungkinan keputusan, yaitu menolak hipotesis nol dan gagal menolak hipotesis nol. Keputusan uji statistik dapat menggunakan dua pendekatan, yaitu pendekatan klasik dan pendekatan probablistik.
Pendekatan klasik adalah keputusan uji statistik yang dilakukan dengan cara membandingkan nilai perhitungan uji statistik dengan nilai pada tabel.
Nilai tabel yang dilihat sesuai dengan jenis distribusi uji yang kita lakukan. Besarnya nilai tabel sangat tergantung dari nilai alpha (α) yang kita gunakan dan juga tergantung pada arah hipotesisnya, satu sisi (one tail) atau dua sisi (two tail).
Kriteria dalam memutuskan apakah hipotesis nol ditolak atau gagal ditolak adalah:
- Bila nilai perhitungan uji statistk lebih besar dibandingkan nilai tabel (nilai perhitungan > nilai tabel), maka keputusannya Ho ditolak.
- Bila nilai perhitungan uji statistk lebih kecil dibandingkan nilai tabel (nilai perhitungan < nilai tabel), maka keputusannya Ho gagal ditolak.
Pendekatan probabilistik adalah keputusan uji statistik dengan cara membandingkan nilai P dengan nilai alpha (α).
Ketentuan yang berlaku adalah sebagai berikut:
- Bila nilai P < nilai α, maka keputusannya Ho ditolak.
- Bila nilai P > nilai α, maka keputusannya Ho gagal ditolak.
Nilai P merupakan nilai yang menunjukkan besarnya peluang salah menolak Ho dari data penelitian. Harapan kita nilai P adalah sekecil mungkin.
Dengan nilai P kecil, kita yakin bahwa adanya perbedaan pada hasil penelitian menunjukkan pula adanya perbedaan di populasi.
BACA JUGA: Tahap Lengkap Membuat Proposal Penelitian
Kesimpulan
Jadi, pengertian Uji hipotesis merupakan salah satu cara dalam menarik kesimpulan terhadap parameter populasi. Sehingga prinsip dari uji hipotesis ini adalah membandingkan antara nilai sampel (data hasil penelitian) dengan nilai hipotesis (nilai populasi) yang diajukan. Dalam uji hipotesis ini selalu dihadapkan pada dua kesalahan, yaitu kesalahan tipe I (α) dan kesalahan tipe II (β) dan tidak mungkin dapat dielakkan, namun dapat diminimalisir, sehingga dalam melakukan uji hipotesis harus mengikiti prosedur atau kaidah secara benar.
FAQ

Karena dengan adanya hipotesis arah dan tujuan penelitian akan terlihat jelas dan dapat ditentukan.
Tentunya hipotesis diperlukan apabila didalam penelitian mempersoalkan hubungan antarvariabel.
Sebenarnya hipotesis bisa saja tidak dimiliki oleh seorang peneliti, dengan mengemukakan jenis tersebut masuk dalam kategori penelitian deskriptif.
Tentunya jawabanya adalah tidak. Karena benar atau tidaknya sebuah hipotesis tidak ada kaitannya dengan terbukti dan tidak terbukti tentang hipotesis.
Dalam penelitian dalam pengembangan tidak melakukan deskripsi merupakan suatu fenomena pada diri suatu objek. dan tentunya juga tidak menggunakan uji hipotesis.







